ANOVA와 사후검증 (완전이해~~^^)
통계분석 2011. 11. 24. 11:50 |ANOVA 에서 유의한 차이가 있는 경우 Tukey, Duncan, Scheffe 등의 사후분석(Post-Hoc test)를 하게 된다.
문제는 ANOVA 와 사후분석 결과가 일치하지 않는 경우가 종종 나올 때, 어떻게 해야되는지 고민을 하게 된다. 2가지 예를 들어 상황을 살펴보도록 한다.
1. ANOVA 에서는 유의하지 않은데, 사후분석에서 유의하게 나온 경우
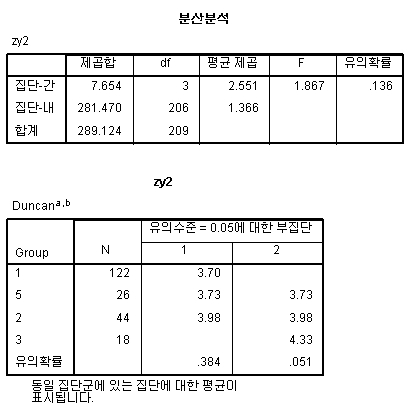
위의 결과를 보면 ANOVA 결과, 집단간 유의한 차이가 없는 것으로 나타났다(p=.136>.05).
하지만, Duncan 의 사후분석에서는 3 Group(M=4.33) 이 1 Group(M=3.70) 보다 높은 것으로 나와, 서로 상반된 결과를 보이고 있다.
이와 같이 ANOVA 에서는 유의하지 않지만, 사후분석에서는 유의한 경우에는 사후분석의 결과를 무시한다.
2. ANOVA 에서는 유의한데, 사후분석에서 유의하지 않은 경우
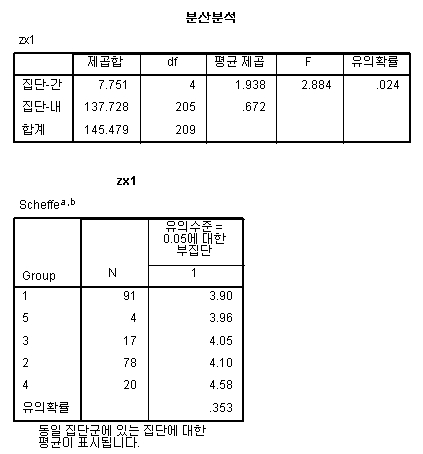
사실 1과 같은 경우에는 큰 문제가 되지 않는다. 보통 연구자들은 ANOVA 에서 유의하지 않은 경우 사후분석을 하지 않기 때문이다.
2와 같이 ANOVA 에서는 유의한데, 사후분석에서 유의하지 않게 나온 경우 난감해하는 연구자들이 많다.
위의 경우, 집단간 유의한 차이가 있는 것으로 나타났다(p=.024<.05).
그러나, Scheffe의 사후분석에서는 유의하지 않게 나온 경우이다.
이때, 연구자들이 먼저 생각하는 것은 사후분석 방법을 바꿔서 다시 분석하는 것이다. Duncan 이나 LSD 등의 경우에는 사후분석 결과를 좀 관대하게 보는 경향이 있어, 대부분 연구자들이 원하는 결과를 얻어준다.
하지만 이러한 방법(사후분석을 바꾸는 방법)은 사실 매우 위험한 작업이다. 한 논문(or 보고서)에서는 일관성을 유지해야 한다. 중간에 분석 방법 등을 바꿀 경우에는 그에 타당한 이유가 있어야 한다. 문제는 사후분석 종류를 바꾸는 타당한 근거를 제시하는 것은 거의 불가능에 가깝다. 따라서 전체적으로 Scheffe의 사후분석을 했다면 이 경우에도 Scheffe 의 사후분석을 해야 한다.
그러면 어떻게 제시를 하고, 해석을 해야 하는지 고민해야 한다.
가장 정확한 답변은 있는 그대로 기술하는 것이다. 즉, ANOVA 에서는 유의했지만, Scheffe 의 사후분석에서는 유의하지 않게 나온 것을 표에 그대로 기재하는 것이다.
ANOVA 에서 주 분석 결과는 ANOVA 이다. 따라서 ANOVA 결과를 먼저 제시하여야 하는 것이며, 사후분석은 추가적인 분석이므로 ANOVA 에서 유의하지 않았다면 사후분석 결과를 볼 필요 자체가 없는 것이고, ANOVA 에서 유의했는데, 사후분석에서 유의하지 않았다면 집단간 유의한 것으로 해석을 하면 된다.
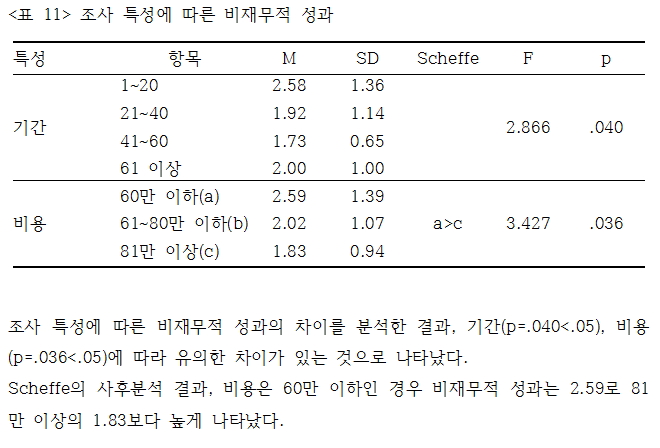
위와 같이 기술할 수 있다.
즉, ANOVA 와 사후분석에서 모두 유의하게 나온 비용의 경우에는 그대로 설명을 하고, ANOVA 에서는 유의하지만 사후분석에서는 유의하지 않게 나타나 기간은 ANOVA 결과에서는 유의하다고 설명하는 것이다.
이와 같이 기술하는 것이 가장 보편 타당하다.
다만, 연구자의 입장에서는 기간에 다른 비재무적 성과는 유의한 차이가 있는데(p=.040<.05), 사후분석에서 유의하지 않아서 그 차이를 설명하지 못하는 것에 대해 아쉬울 수 있다. 이때 가능한 방법으로 ANOVA 결과 유의하다는 것은 집단간에 어느 곳에서인가 유의한 차이가 있다는 것이다. 다만 사후분석에서 유의하지 않게 나왔을 뿐이다. 이것은 다시 생각하면 기간에서 평균이 가장 높은 1~20 일의 2.58과 가장 낮은 41~60일의 1.73 간에는 차이가 있다. 따라서 다음과 같은 해석도 무방하다.
기간에 따른 비재무적 성과는 유의한 차이가 있다(p=.040<.05). 기간이 20일 이하의 비재무적 성과는 2.68로 41~60일의 1.73 보다 높게 나타났다.
여기서 주의 사항은 Scheffe 의 사후분석이라는 것을 쓰면 안된다는 것이다. 이 말은 Scheffe 에서 유의한 경우에만 사용 가능하다.
- 이일현 박사님이 쓰신글입니다


